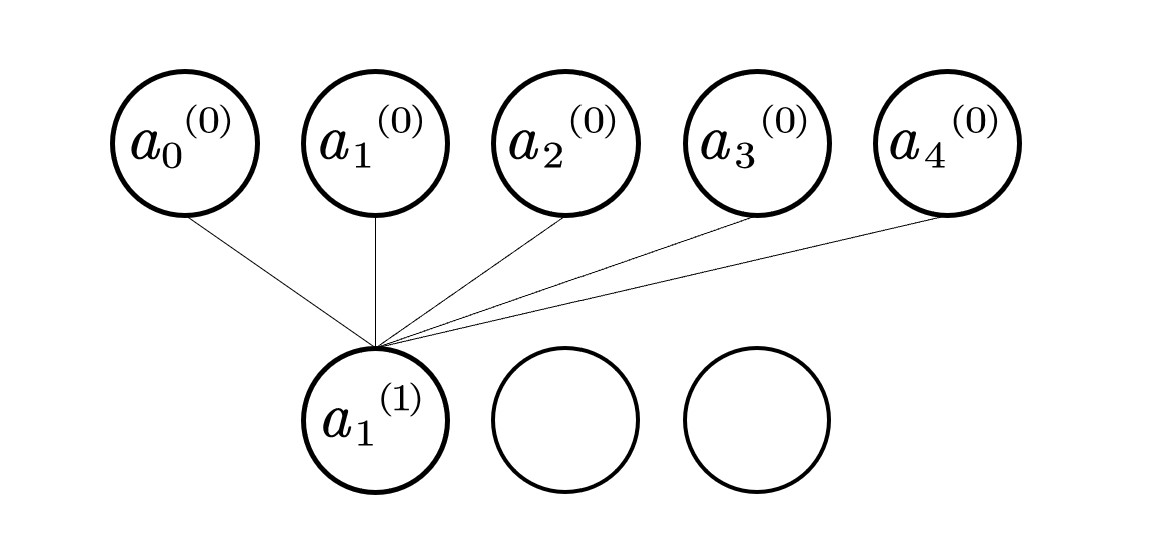
\( a_0^{(1)}=\sigma (w_{0,0}a_0^{(0)}+w_{0,1}a_1^{(0)}+...+w_{0,n}a_n^{(0)}+b_0) \)
即
\( \sigma \left( \left[ \begin{array}{l} w_{0,0}& w_{0,1}& ...& w_{0,n}\\ w_{1,0}& w_{1,1}& ...& w_{1,n}\\ ...& ...& ...& ...\\ w_{k,0}& w_{k,1}& ...& w_{k,n}\\ \end{array} \right] \left[ \begin{array}{c} {a_0}^{\left( 0 \right)}\\ {a_1}^{\left( 0 \right)}\\ ...\\ {a_n}^{\left( 0 \right)}\\ \end{array} \right] +\left[ \begin{array}{c} b_0\\ b_1\\ ...\\ b_k\\ \end{array} \right] \right) =\left[ \begin{array}{c} {a_0}^{\left( 1 \right)}\\ {a_1}^{\left( 1 \right)}\\ ...\\ {a_k\\\\++}^{\left( 1 \right)}\\ \end{array} \right] \)
其中b0为偏置。
常见激活函数:
1. sigmoid:(0,1)
2. tanh:(-1,1)
3. relu:max(0,x)
4. ELU:a(e^x-1)
对于某个数据x,由一个模型f,使之生成预测值\(f(x,w)=Y_{predict}\)。
为判断模型好坏,通过对比预测值与实际值,引入损失函数(均方误差)
\( loss=(Y_{predict}-Y_{true})^2 \qquad (回归损失) \\ loss=Y_{true} \cdot \log Y_{predict} \qquad (分类损失) \)
通过调整参数\(w\),尽可能降低\(loss\)。
选择起始点\(w_0\),调整\(w_0\)的位置,让\(loss\)不断减少。
1. 计算w的梯度(导数)
\( \nabla w=\cfrac{f\left( w+0.0000001 \right) -f\left( w-0.0000001 \right)}{2\times 0.0000001} \)
2. 更新\(w\)
\( w=w-\alpha \nabla w \)
其中:
1. \(\nabla w < 0\),意味着\(w\)将增大;
2. \(\nabla w > 0\),意味着\(w\)将减小。
若有一个函数\(J(a,b,c)=3(a+bc)\),令\(u=a+v\),\(v=bc\),则可绘制计算图为:
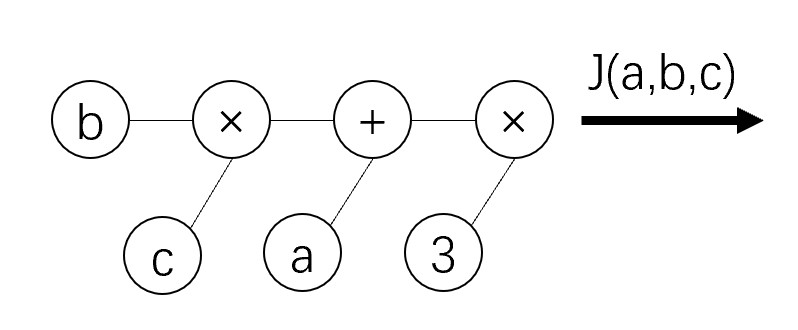
此时可以清楚地对每个节点求偏导。
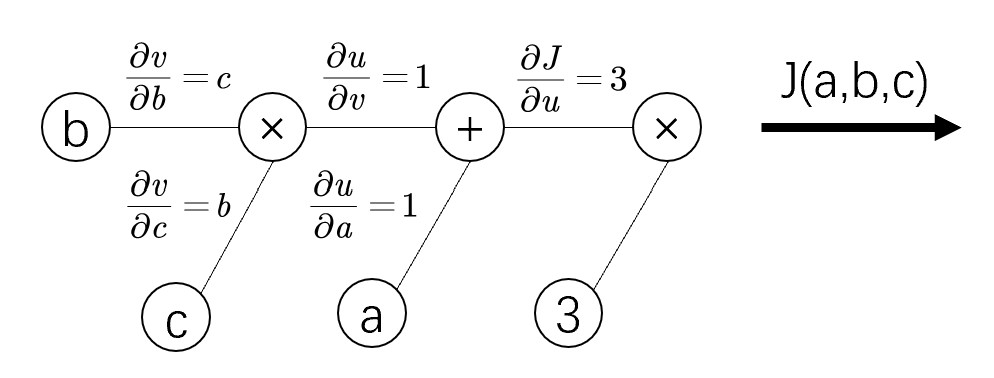
反向传播的过程即上图从右到左的过程,自变量a,b,c各自的偏导为连线上梯度的乘积。
\( \cfrac{\partial J}{\partial a}=\cfrac{\partial J}{\partial u}\cfrac{\partial u}{\partial a}=3\times 1 \\ \cfrac{\partial J}{\partial b}=3\times 1\times c \\ \cfrac{\partial J}{\partial c}=3\times 1\times b \)
\(w_1,w_2,...,w_n\)表示网络第n层的权重,\(w_n[i,j]\)表示第n层第i个神经元连接到第n+1层第j个神经元的权重。
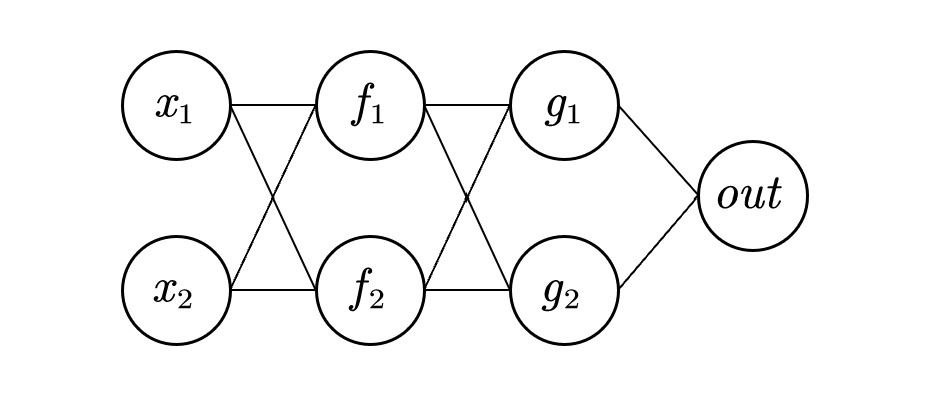
此时\(f_1=w_1[1,1]x_1+w_1[2,1]x_2\),\(f_2=w_1[1,2]x_2+w_1[2,2]x_2\),以此类推。因此可以画出此神经网络的计算图
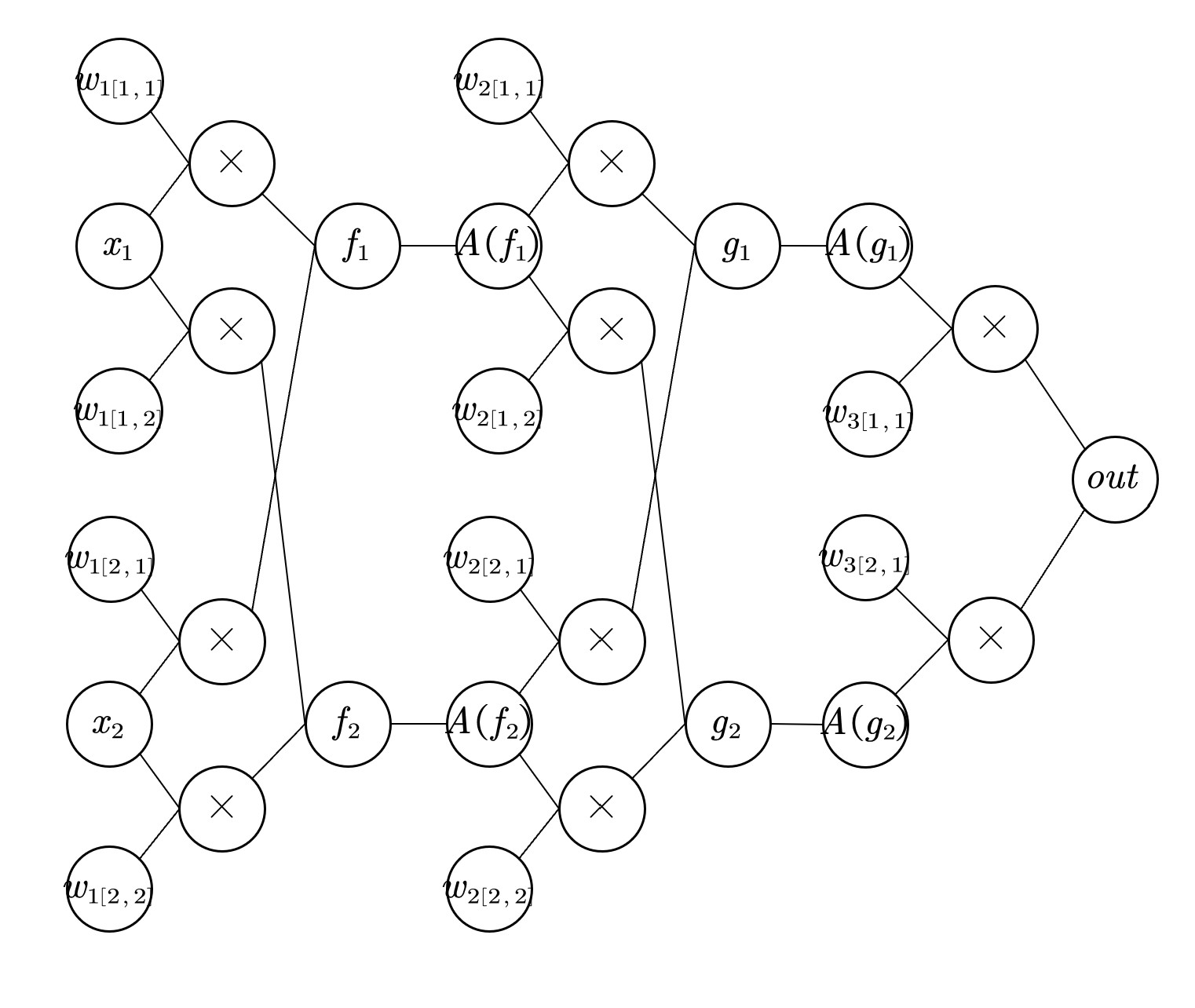
其中函数A为激活函数。得到out后即可得到loss,调整\(w\),使得loss接近0。此处考察\(w_1[1,2]\)的变化对loss的影响
\( \cfrac{\partial loss}{\partial w_1\left[ 1,2 \right]}=x_1A^{\prime}\left( f_2 \right) \left( w_2\left[ 2,1 \right] A\prime\left( g_1 \right) w_3\left[ 1,1 \right] +w_2\left[ 2,2 \right] A\prime\left( g_2 \right) w_3\left[ 2,1 \right] \right) \times \nabla out \)
其中\(\nabla out = \cfrac{\partial loss}{\partial out}\).
如果要逐个计算\(\frac{\partial loss}{\partial w}\),需要的内存非常大。而反向传播的思想是从out向前逐层计算,先计算最后一层的梯度,再用最后一层的数据计算倒数第二层的梯度,以此类推。
对于pytorch中的一个tensor,需要设置属性.requires_grad=True,此时将追踪对张量的所有操作(即tensor的变化量),方便后续计算梯度。
tensor = torch.ones(n,m,requires_grad=True)
如果不想记录某个操作,请使用torch.no_grad()
with torch.no_grad(): tensor = torch.randn(n,m)
在训练模型的代码中需要使用requires_grad=True,但在其他区域(如评估模型)不需要进行梯度计算,为防止跟踪历史记录以及过度使用内存,请在合适的区域使用torch.no_grad()。
import torch in = torch.randn(2,2,requires_grad=True) #创建输入变量 var1 = in + 2 #中间变量1 var2 = var1*var1*3 #中间变量2 out = var2.mean() #输出 out.backward() #反向传播 in.grad #输出对输入的梯度
当输出为标量时,可以调用backwad()方法,但输出为向量时,调用backward()时还需要传入其他参数。
import numpy as np
import torch
import matplotlib.pyplot as plt
learning_rate = 0.01
#准备数据
#y = 3x + 0.8
x = torch.rand([50,1])
y_true = x*3 + 0.8
#通过模型计算y_predict
w = torch.rand([1,1],requires_grad=True)
b = torch.tensor(0,requires_grad=True,dtype=torch.float32) #只有浮点型张量可以指定梯度
#通过循环反向传播更新参数
for i in range(2000):
# 计算loss
y_predict = torch.matmul(x, w) + b # matmul为矩阵乘法
loss = (y_true - y_predict).pow(2).mean() #pow为幂次
if w.grad is not None: #.grad为累加型,需要归零
w.data.zero_()
if b.grad is not None:
b.data.zero_()
loss.backward() #反向传播
w.data = w.data - learning_rate*w.grad #向梯度方向前进一个小量
b.data = b.data - learning_rate*b.grad
if i%500 == 0:
print("w,b,loss",w.item(),b.item(),loss) #每100次输出一个结果
plt.figure(figsize=(20,8))
plt.scatter(x.numpy().reshape(-1),y_true.numpy().reshape(-1))
plt.plot(x.numpy().reshape(-1),y_predict.detach().numpy().reshape(-1))
plt.show()
nn.modul是torch.nn的一个类,是自定义网络的一个基类。
自定义网络时,有两个方法需要特别注意
1. __init__需要调用super方法,继承父类的属性和方法
2. farward方法必须实现,用来定义网络的向前计算的过程
用y=wx+b模型举例如下
from torch import nn class Lr(nn.Module): def __init__(self): super(Lr,self).__init__() #继承父类init参数 self.linear = nn.Linear(1,1) def forward(self,x): out = self.linear(x) return out
nn.Linear为torch预定义的线性模型,即全链接层,传入的参数为输入的数量,输出的数量(in_features,out_features)。
nn.Module定义了__call__方法,实现的就是调用forward方法,即Lr的实例。
# 实例化模型 model = Lr() # 传入数据,计算结果 predict = model(x)
优化器(optimizer),可以理解为更新参数的方法,比如常见的随机梯度下降(stochastic gradient desent, SGD)
优化器类是由torch.optim提供的,例如
1. torch.optim.SGD(参数,学习率)
2. torch.optim.Adam(参数,学习率)
参数可以通过model.parameters来获取,获取模型中所有requires_grad=True的参数。
优化类的使用方法:
1. 实例化
2. 将所有参数的梯度值置为0
3. 反向传播计算梯度
4. 更新参数值
示例如下:
optimizer = optim.SGD(model.parameters(), lr=1e-3) # 实例化 optimizer.zero_grad() # 梯度置为0 loss.backward() # 计算梯度 optimizer.step() # 更新参数
1. 均方误差:nn,MSEloss() # 常用于分类问题
2. 交叉熵损失:nn.CrossEntoptLoss() #常用于逻辑回归
使用方法
model = Lr() # 实例化模型 criterion = nn.MSELoss() # 实例化损失函数 optimizer = optim.SGD(model.parameters(), lr=1e-3) # 实例化优化器类 for i in range(100) y_predict = model(x_true) #向前计算预测值 loss = criterion(y_true,y_predict) #计算损失结果 optimizer.zero_grad() # 当前循环参数梯度置为0 loss.backward() # 计算梯度 optimizer.step() # 更新参数
import torch
from torch import nn
import torch.optim as optim # 修正拼写错误
import numpy as np
import matplotlib.pyplot as plt
# 1. 定义数据
x = torch.rand([50, 1])
y = x * 3 + 0.8
# 2. 定义模型
class Lr(nn.Module):
def __init__(self):
super(Lr, self).__init__()
self.linear = nn.Linear(1, 1) # 创建一个线性层,输入维度为1,输出维度也为1
def forward(self, x):
out = self.linear(x)
return out
# 3. 实例化模型、损失函数和优化器
model = Lr()
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=1e-3)
# 4. 训练模型
for i in range(100):
out = model(x)
loss = criterion(y, out)
optimizer.zero_grad()
loss.backward()
optimizer.step()
if (i + 1) % 20 == 0:
print(f"Epoch [{i+1}/100], Loss: {loss.item():.6f}")
# 5. 模型评估
model.eval()
predict = model(x)
predict = predict.data.numpy()
plt.scatter(x.data.numpy(), y.data.numpy(), c="r")
plt.plot(x.data.numpy(), predict) # 修正拼写错误
plt.show()
哔哩哔哩:Python-知识库:【Pytorch入门到实战】卷积神经网络、循环神经网络、机器学习、深度学习、AI人工智能全套学习教程(附项目实战源码)一口气全都学完!